By Allan Millar
By Allan Millar
Over the course of my next few articles, I will be looking at the Equity Risk Premium. To begin with, we will ask what it is. This will be followed by a brief look at its importance, historical and prospective value, as well as a consideration of the impact of behavioural economics. Finally, we will look at a UK data set to consider prospective values and the ways in which they may be calculated.
The Equity Risk Premium is relevant at the moment as its key elements, equities and bonds, are being influenced by political as much as economic events. It also coincides with an unusual period in financial history where it is difficult to determine what a risk-free asset is, precipitated by the financial and Eurozone crises, and there is a current debate about the death of the cult of equities. On this topic, Bill Gross of Pimco stated to the Wall Street Journal (31st July 2012) that “consistent, annual returns” are a thing of the past and that the 6.6% inflation adjusted annual gain since 1912 is a “historical freak.” Gross’s comments are reminiscent of the famous BusinessWeek cover pronouncing the death of equities in August 1979. At that point the Dow sat at 875; it is now at circa 13,420.
That of course can be contrasted with the Atlantic Monthly in 1999, which heralded Dow 36,000 (an allusion to James K. Glassman and Kevin Hassett’s book and market prediction, Dow 36,000). As we know, shortly afterwards, the dotcom bubble and the events of 9/11 had a dramatic effect on stock indices across the globe. On the other side of the equity risk premium we have bonds and with that in mind it is also worth considering what has been happening over the last few years. According to Bloomberg (24th June 2012), the Bank for International Settlements said that government “bonds losing their risk-free status are depriving investors of wealth-preservation opportunities as Europe’s debt crisis boosts demand for havens.” This actually referred to a reduction in the number of safe havens, with US Bonds being the beneficiaries of safe-haven status. So much so that over a year after the US Credit Rating was downgraded by Standard and Poor’s the yields on 5, 10 and 30-year bonds are all now lower. These factors all influence the risk premium and my principal aim is to examine some of the extensive literature on the subject, picking out the key concepts, and then quantifying and empirically testing some of the key assumptions on some UK specific data. The objective of a later article will be to calculate the Equity Risk Premium in the UK from 1976 to 2012 and attempt to determine a value for the prospective premium.
What is the Equity Risk Premium?
Defining the Equity Risk Premium (ERP) and putting a value to it has been an issue for many years. There is consensus that it has been overstated but to what degree? Mehra and Prescott (1985 p145) wrote that “Historically the average return on equity has far exceeded the average return on short-term virtually default-free debt.” They mention that when one looks at the S&P over the period 1889 to 1978, the ERP is 6.18%. This is interesting, given what we will look at later with regard to other contributors to this debate and to specific UK data. The premise of their work is that large equity returns and low returns on risk-free assets will prevail (p.145) in “an equilibrium model which is not an Arrow-Debreu economy”. An in-depth analysis of the equilibrium model is not in the scope of this article, however Mehra and Prescott (1985) reinforce their assertion that this is not realistic by stating that (p.146) “some equilibrium model with a friction will be the one that successfully accounts for the large average equity premium. Xu (2009) also notes that the historical data points to a degree of risk aversion that is not supported by theoretical models. Constantinides (2006 p.1) adds that the theory suggests “the risk premia of financial assets are explained by their covariance with per capita consumption growth.” He goes on to say however that “per capita consumption growth covaries too little with the returns of most classes of financial assets and this creates a whole class of asset pricing puzzles.” With regard to Arrow-Debreu, Constantinides (2006 p.37) adds that “The fictitious representative consumer that holds all the stock market and bond market wealth does not face credible borrowing constraints.” This supports Mehra and Prescott’s conclusion on this particular equilibrium model.
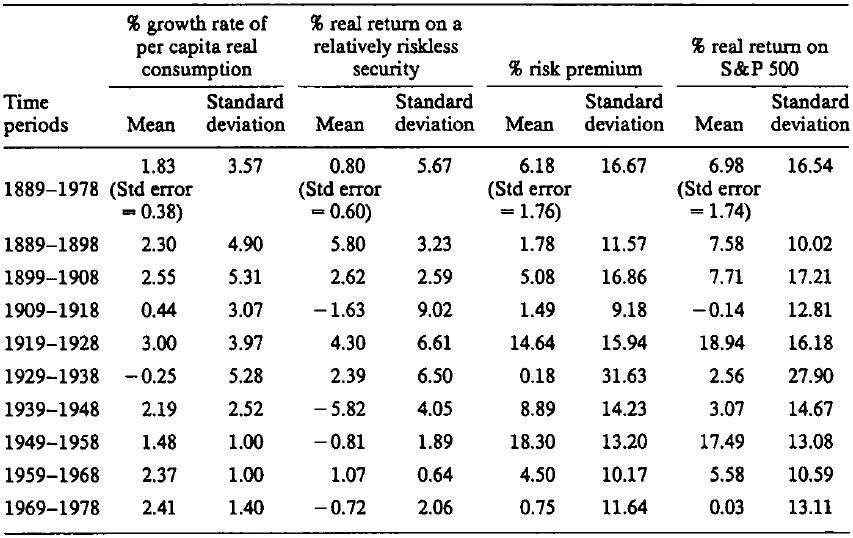
Mehra and Prescott (1985 p.147) also include a table which is very valuable as it clearly illustrates how volatile the Equity Risk Premium is and the importance of time. Figure 1 indicates that the ERP from 1889 to 1978 was 6.18%, but we can see how this has fluctuated from -0.14 in the period 1909 to 1918 to 18.94 from 1919 to 1928. Other commentators on the ERP have made this observation and it is of fundamental importance to investors, as well as those making wider financial decisions on the risk premium, such as capital investment. We should also consider however that the risk premium required by investors will vary over time and the results in the table reflect sample variations within the distribution. The importance of time and volatility will be examined with particular regard to UK data in a later article. Click charts to enlarge.
Figure 1: Mehra and Prescott (1985 p.147)
It is interesting to note the analysis above and Mehra and Prescott (1985) conclude their research by raising the following question (p.158): “The equity premium puzzle may not be why was the average equity return so high but rather why was the average risk-free rate so low.” It is an important conclusion and one which we will look at later with regard to the FTSE All Share and an index of total UK Government Gilt Returns.
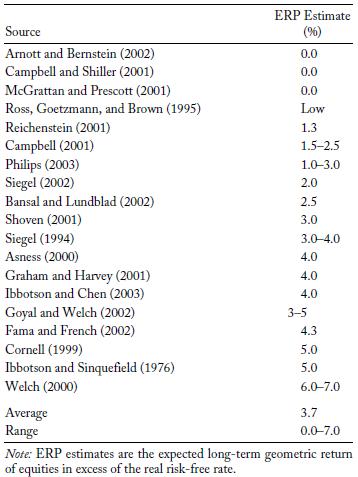
In addition to the information from Mehra and Prescott, the Research Foundation of the CFA published the following values, (Figure 2), in their 2011 paper, reflecting on their estimates in 2001. The authors, Hammond and Leibowitz, observe that (p.15) “the ERP, far from being a settled matter, continues to challenge analysts.” They note that four issues complicate the matter:
- The definition of ERP
- The approach taken, (p.15) “objective, circumstantial or behavioural”.
- The different circumstances facing investors at different times
- A combination of the first three issues
Given these factors, it is not a surprise to see that the experts listed below had Equity Risk Premium estimates ranging from 0% to 7%.
Figure 2: Estimates as of 2001 of the ERP (CFA Institute 2011)
As well as being difficult to determine, the ERP is also one of the most important features of Finance and it has been extensively covered by a number of esteemed academics. Perhaps the most comprehensive review was undertaken by Dimson, Marsh and Staunton in their 2002 work “Triumph of the Optimists.” This is most interesting when we consider the Equity Risk Premium puzzle and in their work they highlighted some of the key issues surrounding the ERP, and these: what is the historical ERP, how is it calculated and what will it be in the future, will be the foundation for the latter part of this paper. Their study was extensive and took in 101 years of data across sixteen nations; my scope will be slightly more limited, looking in detail at the UK. To begin and by way of a definition, they stated that downside volatility is not very popular with investors and consequently, any investment in equities must be able to provide adequate compensation for the attached risk, the risk being relative to investing in a risk-free asset. Historically, risk free assets have been government bonds. It therefore follows that the difference in return between equities and bonds is the Equity Risk Premium. In simple terms:
ERP = expected return for equities – risk free rate
As we have seen in recent months, government bonds may not be the “risk free” asset they were once considered to be and this issue will be addressed later in this paper. Dimson et al also make the point that we can measure the ERP in two ways, firstly against short-term government securities or long-term bonds. It is their assumption that the former is preferable (p.163), “only treasury bills can really be considered risk-free”. This point is clarified by the mention that hyper-inflation may “cause even bill investors to experience large losses in real terms”. They also state another key feature of the Equity Risk Premium, that it is an important variable as it is an essential component used in projecting investment returns in the future and is used for (p.163) “calculating the cost of equity capital for companies, valuing companies and shares, appraising investment proposals and determining fair rates of return for regulated businesses.”
This view is endorsed by Damodaran (2011 p.2) who wrote: “Equity risk premiums are a central component of every risk and return model in finance and are a key input into estimating costs of equity and capital in both corporate finance and valuation.” To highlight this, Damodaran also provided a table, highlighting the ERP’s role in four important financial models:
Figure 3: Damodaran (2011 p.5)
Damodaran notes that each of these four models needs a risk premium input and also a risk free rate, which may be difficult to determine today. As discussed, do we look at 3 and 6 month bills, 5 or 10 year bonds? Of fundamental importance though is the Equity Risk Premium. Damodaran (2011) points out that the size of the ERP will determine the expected returns and value of investments which are not risk free. He goes on to say (p.5) “Consequently, the choice of an equity risk premium may have much larger consequences for value than firm-specific inputs such as cash flows, growth and even firm-specific risk measures (such as betas).” This has obvious implications across companies as any investments they make will need to generate a higher return than their cost of capital. Therefore, if the ERP increases, there may be a reduction in investment as a sufficient return cannot be generated as the cost of capital will have increased.
Welch (2000 p.501) provides another perspective, also incorporating the Capital Asset Pricing Model (CAPM), describing the ERP as “perhaps the single most important number in financial economics”. He continues by saying that it impacts upon investment decisions, “how much of one’s portfolio an investor should put into stocks versus bonds.” To incorporate the CAPM and acknowledge its importance in finance, he explains that it is used “in computing an appropriate hurdle rate for accepting investment projects”.
Ibbotson (2011, p18) provides another view, describing the ERP as the “ long-run equilibrium concept that gives an estimate of the future excess return of the stock market over and above the bond market.” This raises an important point, how do we gauge what the premium for risk should be? This is one of the topics we will return to. Similar to Dimson et al and Damodaran, Grinold, Kroner and Siegel (2011, p.53) say that the ERP “is almost certainly the most important variable in finance” as it is essential to saving and asset allocation decisions. But, importantly, they add (p53) that “recognised experts cannot agree on the ERP’s value within an order of magnitude or even agree whether it is negative or positive.” This is a key point, also raised by Dimson et al (2002 p.175) who said, “the risk premia estimated in this study….are around 1.5% lower than those that have been reported in previous studies.
This point is also reinforced by Damodaran (2011 p.2) who added: “it is surprising how haphazard the estimation of equity risk premiums remains in practice”. Welch (2000 p.502) also details this issue by saying that there is no agreement on the correct equity premium and, importantly, there is no “consensus on how it should be estimated”. Taylor (www.globalfinancialdata) summarises these views by stating that there is no agreement on the value of the ERP because it “is not a number whose value is fixed, because it changes over time”. Cochrane (2011 p.1048) says that “The economic question is, “How much do expected returns vary over time?” There will always be lots of unforecastable return movement, so the variance of ex post returns is not a very informative comparison for this question.” Taylor (www.globalfinancialdata) goes on to discuss why it is difficult to determine a value for the Equity Risk Premium, pointing out that looking to the future is very difficult, what will the returns be on bonds and shares? To estimate this we need to look back and that also presents us with issues. The two key points are the date we start from and the length of time we invest for. As Taylor (www.globalfinancialdata.com) points out, this will give different values if your start date is 1929 or 1932, is it a 10 year period or a 30 year period? Even within time periods, the start date is crucial. Dimson et al (2002 p.163) also reflect on the fact that “the historical risk premium is often treated as a proxy for the prospective risk premium” and their work suggests that it has been overestimated. Following on from this, Ilmanen (2011) asks which method is best to predict the future ERP. As we have seen, the most commonly used method has been looking at past returns and Ilmanen states (p.101) that practical and theoretical lessons “have converted many observers to the belief that expected returns and premiums vary over time”. Given this, we can see that past ERP valuations may not be a particularly good guide to the future. What then is the alternative? Ilmanen concludes that using forward looking valuations are more appropriate, a view endorsed by Cochrane (2011) who argued that changes in the Equity Risk Premium are reactions to changes in investors’ required returns.
Thus far we have assumed that the ERP is calculated on the difference between a return on equities and government bills or bonds. However, there has been some research done recently on whether or not this is appropriate. Work carried out by the economic consultants, NERA, suggests that a better benchmark for the risk free rate would be swaps. In their paper they quote Fabozzi (2004) who highlighted the advantages of this method. Before looking at these points, it is worthwhile to provide a basic explanation of a swap, in this instance, an interest rate swap. Essentially two parties enter into an agreement in which they agree upon a notional sum and agree to pay each other interest on this. For example, they choose US Dollars. One party will pay the other interest payments based upon the swap rate, this is a fixed rate agreed at the start of the contract, and the other party will make payments based on the prevailing LIBOR rate, a topical subject in the summer of 2012. The movement in the LIBOR rate will then determine who benefits from the transaction. It is important to note that the principal is notional, no money changes hands. The transaction proceeds with the exchange of net interest payments. Two of Fabozzi’s points were as follows:
- There are a greater number of maturity points on a swap curve than on the yield curve for bonds, providing the opportunity to calculate the risk-free rate, that is the swap rate, more accurately
- Comparing government bond yields is impacted by the sovereign rating, with interest swaps the risks are similar and make for easier comparison (assuming banks have AA rating or above, this may vary in the current financial climate)
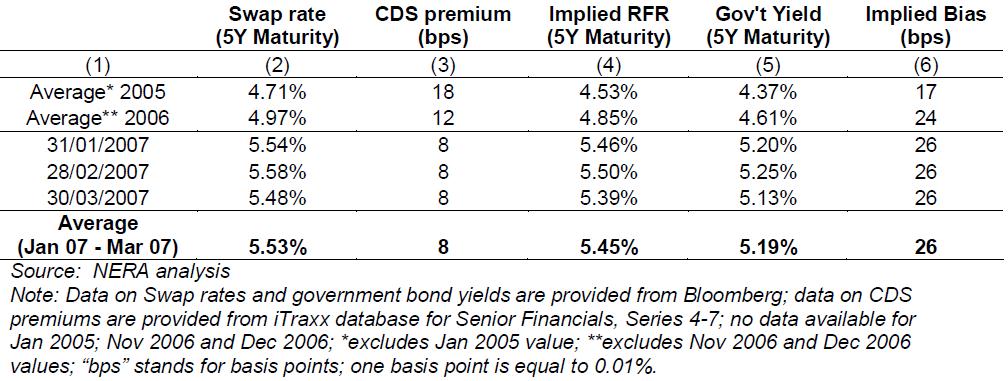
NERA do point out that this is technically not a risk-free rate as there is the chance that one of the counterparties will default on their obligation, this risk is generally covered by a credit default swap. The authors make the assumption that they can determine a market risk with regard to this, allowing them to calculate a risk free rate. This is shown in Figure 4 below:
Figure 4: Implied Bias in UK Government Bond Yields (Using Swap Rates and CDS Premiums)
As can be seen from the data, the risk free rate may be 26 basis points (bps) higher than it would be using government bonds. The authors also point out that this is based on the nominal yield of the gilts and not index linked, with the latter giving a wider gap on average than 26 bps. We will have an extensive look at specific UK data later, but it is worth comparing the monthly risk free rates with the total return on the Conventional Gilts Index which we will use. For the three months in question, the returns were:
January 2007: Monthly -0.81% and Annual -5.36%
February 2007: 0.92% and -4.22%
March 2007: -1.68% and -4.07%
We must remember that these are total returns and NERA are considering yields (this increases the difference between the values). An important conclusion to draw from this, though, is that there are alternative ways in which to calculate the ERP. And, as mentioned, the timeframe is also critical.
In my next article I shall look at historical and prospective values of Equity Risk Premium (ERP), and also the impact of behavioural economics.
References:
• Cochrane, J. 2011. “Discount Rates”. Presidential Address at the 2011 American Finance Association Meeting Journal of Finance, vol. 66, no. 4 (August 2011) pp1047–1108
• Constantinides, George, M. (2006) Understanding the Equity Risk Premium Puzzle Chicago Booth
• Damodaran, A. (2011) Equity Risk Premiums (ERP): Determinants, Estimation and Implications – The 2011 Edition SternSchool of Business
• Dimson, E., Marsh, P., and Staunton, M. (2002) Triumph of the Optimists: 101 Years of Global Investment Returns PrincetonUniversity Press
• Fabozzi, F. (2004) Fixed Income Analysis Frank J. Fabozzi Associates, 2nd Edition.
• Grinold, R.C., Kroner, K.F. and Siegel, L.B. A Supply Model of the Equity Premium Rethinking the Equity Risk Premium (Edited by P. Brett Hammond, Jr., Martin L. Leibowitz, and Laurence B. Siegel) Research Foundation of CFA Institute (2011)
• Ibbotson, R.G. The Equity Risk Premium Rethinking the Equity Risk Premium (Edited by P. Brett Hammond, Jr., Martin L. Leibowitz, and Laurence B. Siegel) Research Foundation of CFA Institute (2011)
• Ilmanen, A. Time Variation in the Equity Risk Premium Rethinking the Equity Risk Premium (Edited by P. Brett Hammond, Jr., Martin L. Leibowitz, and Laurence B. Siegel) Research Foundation of CFA Institute (2011)
• Mehra, R. and Edward C.P. 1985, The Equity Premium: A Puzzle, Journal of Monetary Economics, v15, p145–61.
• Welch, I.Views of Financial Economists on the Equity Premium and on Professional Controversies Journal of Business Vol 73 No 4 2000
• Xu, C. (2009) “ Equity Risk Premium Puzzle And Investors’ Behavioral Analysis —A Theoretical and Empirical Explanation From the Stock Markets in U.S. and China” QMSS G5999 Master Thesis Columbia University
• www.globalfinancialdata.com Taylor, B The Equity Risk Premium | Accessed 4th August 2012
Twitter: @MillarAllan @seeitmarket
Any opinions expressed herein are solely those of the author and do not in any way represent the views or opinions of any other person or entity.