By Max Moore
By Max Moore
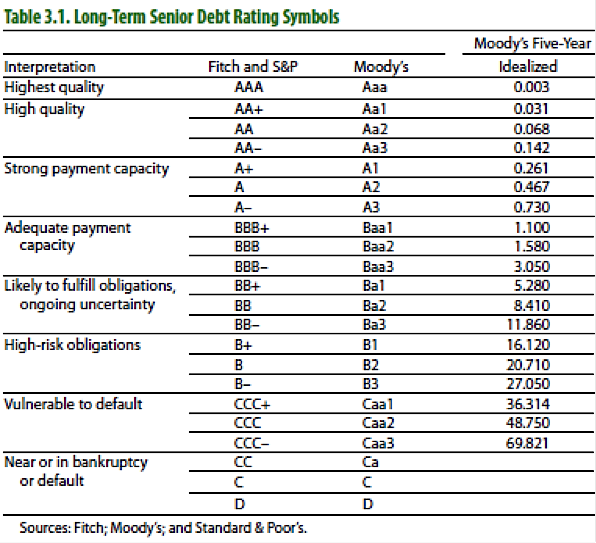
A while back, I did a term project examining the sustainability of Japanese sovereign debt. The ultimate goal of the project was to estimate the effect of a sovereign downgrade on credit default swap (CDS) spreads. In the process, I wound up building a rudimentary CDS pricing model to derive a 5-year default rate, given an assumed recovery rate, risk-free rate and the current market CDS spread. I then linked the derived default rates with a handy table from Moody’s and S&P that scaled the default rates to match a specific long-term senior debt rating. I’ve included both the table from the ratings agencies, as well as a breakdown of the model further down. For this exercise, I focused on European CDS rates.
In a few words, the model allows me to get at CDS implied credit ratings. Almost instinctively, I ran the model on most of the major economies. And to kick 2013 off right, I figured the ratings and related commentary were worth sharing, as they seem much more fitting than the ratings prescribed by the agencies themselves.
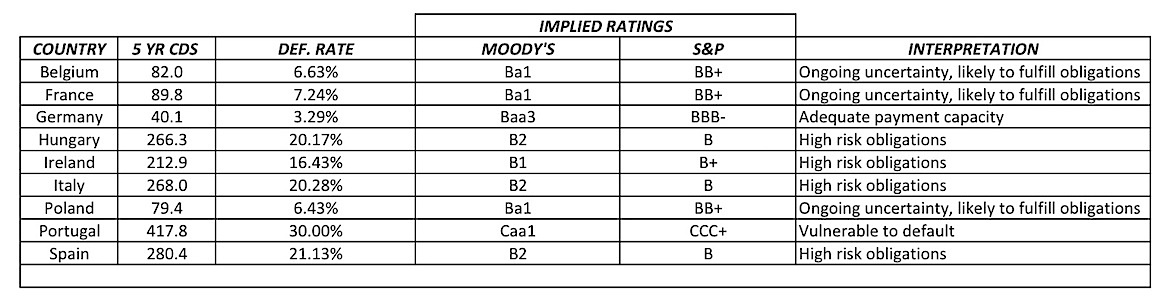
Below are European CDS rates and implied ratings derived from my model for select European countries.
Model Breakdown
For those unfamiliar with what a CDS is, it is a contract that provides insurance against the risk of default (or credit event) by a particular country or company, called the reference entity. As you can imagine, the definition of a credit event is very precise and can cover a technical default or a hard default.
The typical CDS costs nothing to enter, is good for five years and the buyer makes periodic payments to the seller until the earlier of five years or a credit event. The size of the payments is determined by i.) The notional coverage offered by the contract, $n (i.e., the contract will insure $10,000,000 of the reference entity’s debt) ii.) The CDS spread, which is quoted in basis points of the notional value per annum.
Even if a credit event or default occurs, the bonds still have some value depending on the seniority of the debt, the firm’s assets and other factors. As such, the bond holder will recover some of their investment. The percentage of their investment that is recoverable is called the recovery rate, and in this model I’ve used a standardized 40%. A recovery rate of 40% is typically assumed of developed countries while rates as low as 25% are assumed of developing countries. We’ll call the recovery rate R. Since you are only insuring the face value of your investment and would receive R in bankruptcy proceedings, the payout of the CDS is (1-R).
Summarizing to this point, we have protection for 5 years worth (1-R). How much should we pay for protection worth (1-R)? If the reference entity survives, the seller of the CDS makes no payment and received an annual payment from the buyer. Conversely, if it does not survive the seller gives us (1-R). The default probability is the value that makes the total CDS payout $n x (1-R) equal to the market spread in basis points.
So this is the basis for my model and how I came to the European CDS rates and implied credit ratings in the table above. For a more detailed explanation of the model, please contact me via Twitter or through comments below.
Moody’s, S&P Ratings Table with Default Rates
Presented without comment:
Thanks for reading! I’ll be sharing more on this subject in my next article.
Twitter: @maxmoore306 and @seeitmarket
No positions in any of the securities mentioned at the time of publication.